구간합
구간 합은 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘이다.
구간 합 핵심 이론
구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 한다.
합 배열 S 정의
S[i] = A[0] + A[1} + A[2] + ... + A[i-1] + A[i] // A[0]부터 A[i]까지의 합합 배열은 기존의 배열을 전처리한 배열이라 생각하면 된다.
이렇게 합 배열을 미리 구해 놓으면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소한다.
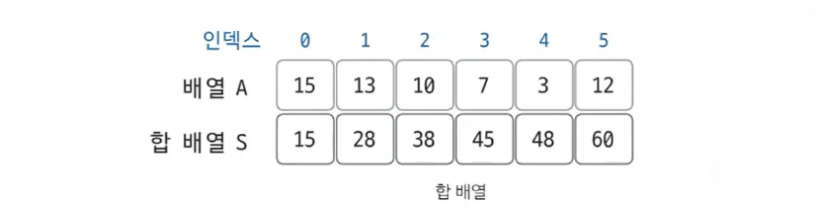
합 배열 없이 배열 합을 구하는 경우, 최악의 경우는 i가 0이고 j가 N인 경우로 시간 복잡도는 O(N)이다.
이런 경우 앞에서 알아본 합 배열을 사용하면 O(1) 안에 답을 구할 수 있다.
합 배열 S를 만드는 공식
S[i] = S[i-1] + A[i]이렇게 구현된 합 배열을 이용하여 구간 합 역시 쉽게 구할 수 있다.
구간 합을 구하는 공식
S[j] - S[i-1] // i에서 j까지 구간 합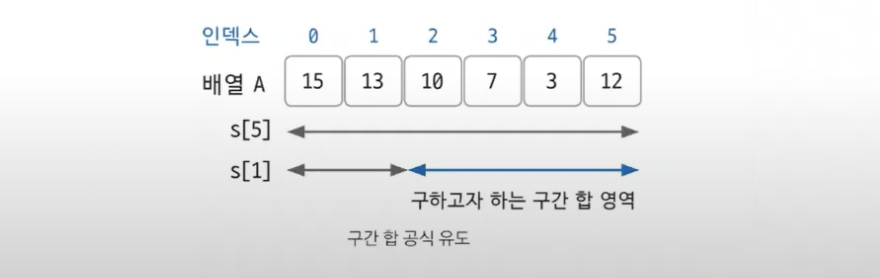
백준 11660번 : 구간 합 구하기5
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
문제
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
1234
2345| 3 | 4 | 5 | 6 |
| 4 | 5 | 6 | 7 |
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
예제 입력 1
4 3
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
2 2 3 4
3 4 3 4
1 1 4 4예제 출력 1
27
6
64예제 입력 2
2 4
1 2
3 4
1 1 1 1
1 2 1 2
2 1 2 1
2 2 2 2예제 출력 2
1
2
3
4BufferedReader로 사용자로부터 input 받기 / N과 M 읽어오기
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BJ_11660 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
...
}
}- StringTokenizer로 한 줄 씩 읽고,
- st.nextToken() 로 한 토큰(띄어쓰기로 구분)씩 읽는다.
- StringTokenizer에 의해 String 값으로 받아와지기 때문에 정수형으로 변환하는 과정이 필요하다.
2차원 배열의 합 배열
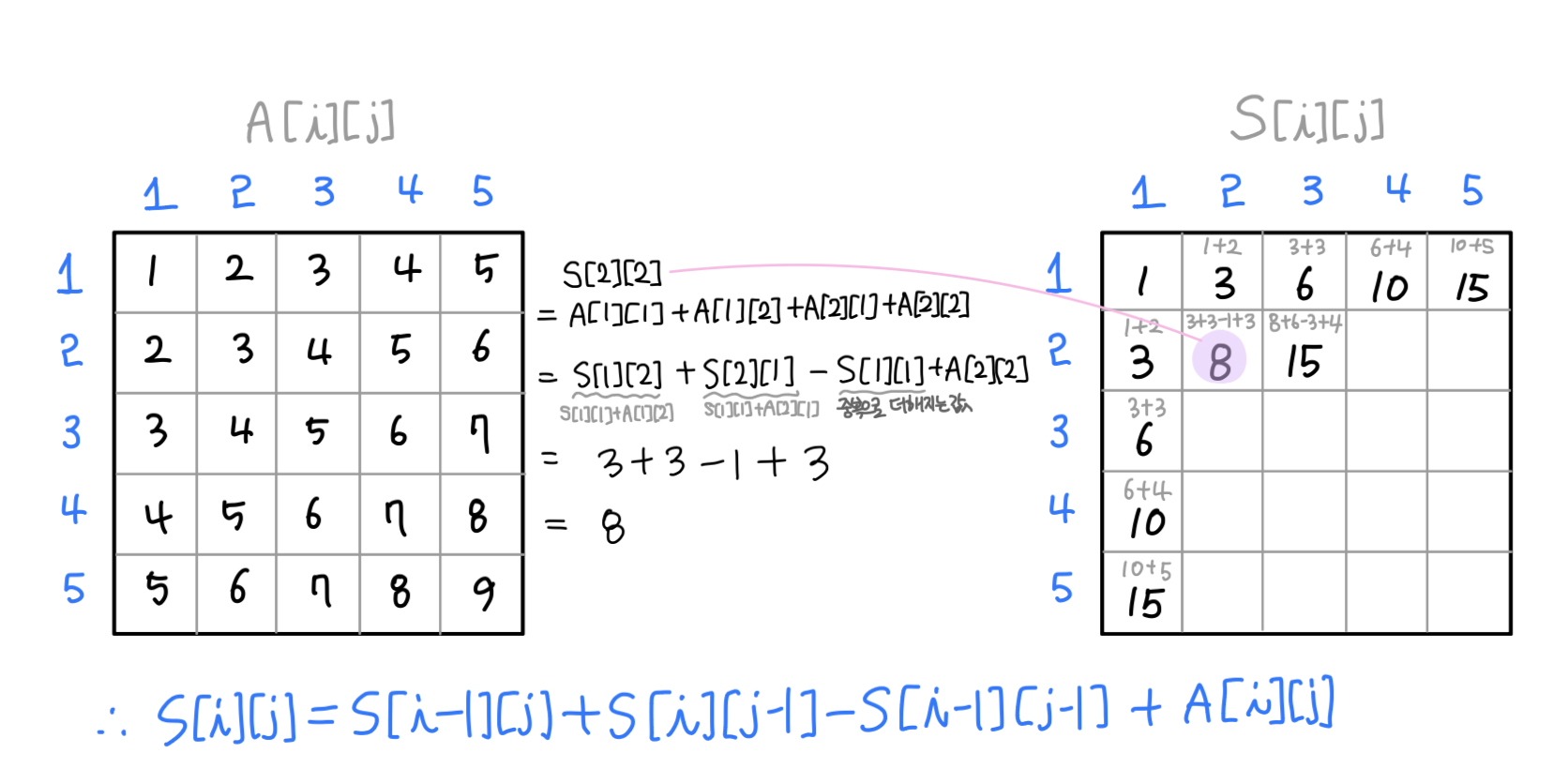
1차원 배열의 합 배열과 달리 2차원 배열에서의 합 배열은
S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j]과 같고, 그림으로 설명하면 위와 같다.
이웃한 두 곳의 합을 더하고, 중복으로 더해진 부분을 다시 빼준 후, 그 자리의 값을 더해준다.
코드로 구현아면 아래와 같다.
long[][] S = new long[N + 1][N + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine()); // 한 줄 씩 읽어오기
for (int j = 1; j <= N; j++) {
S[i][j] = S[i][j - 1] + S[i - 1][j] - S[i - 1][j - 1] + Integer.parseInt(st.nextToken());
}
}
2차원 배열의 구간 합 구하기
- 만약 (2,2)부터 (4,3)까지의 합을 구한다고 하면,
- 아래 그림에서 보듯이, 초록색 구간의 합들을 구해야하는 것이다.
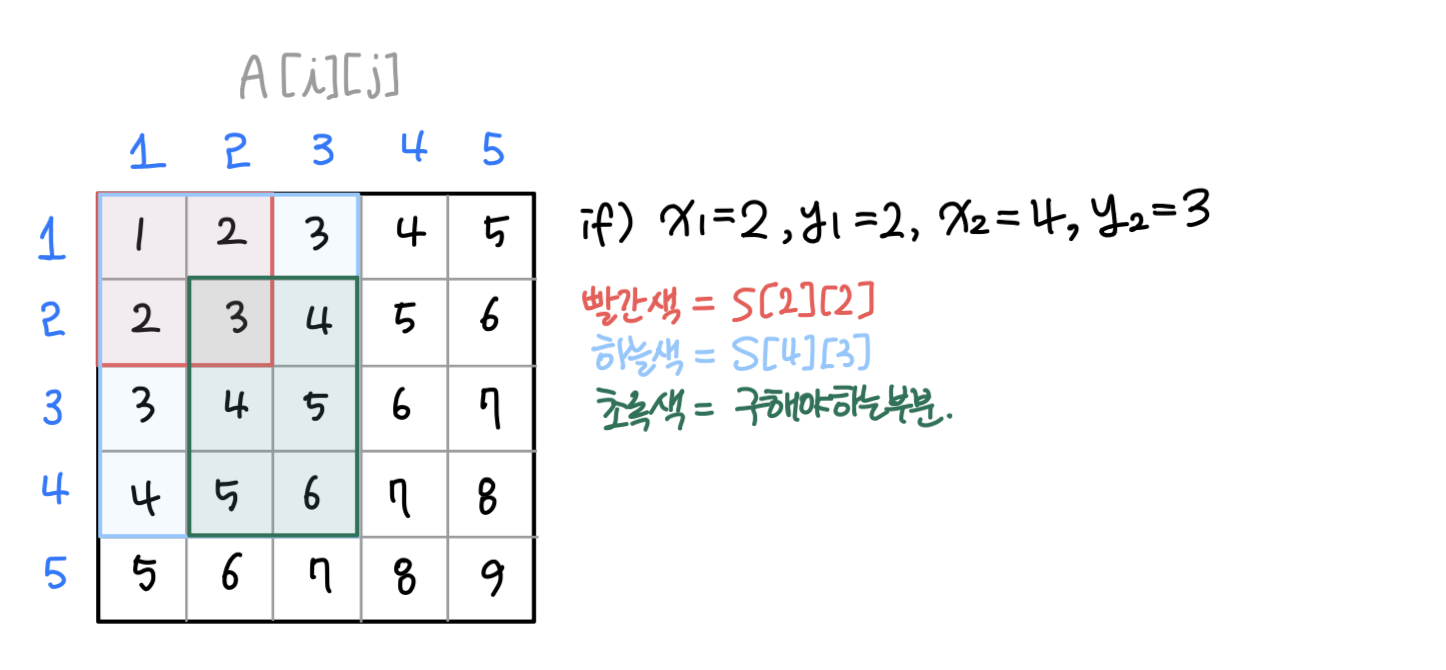
- 위의 예시를 식과 그림으로 표현하면 아래와 같다.

(x1,y1)부터 (x2,y2)까지의 합 공식
S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1-1][y1-1]
코드로 구현하면 아래와 같다.
long result = 0;
for (int q = 0; q < M; q++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
result = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1];
System.out.println(result);
}
전체코드
package back_joon;
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BJ_11660 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
long[][] S = new long[N + 1][N + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
S[i][j] = S[i][j - 1] + S[i - 1][j] - S[i - 1][j - 1] + Integer.parseInt(st.nextToken());
}
}
long result = 0;
for (int q = 0; q < M; q++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
result = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1];
System.out.println(result);
}
}
}
'CODING TEST > Baek-joon' 카테고리의 다른 글
| [ JavaScript (Node.js) ] 백준 실버1 1743번 음식물 피하기 (2) | 2024.03.01 |
|---|---|
| [ JavaScript (Node.js) ] 백준 실버1 1303번 전쟁-전투 (1) | 2024.02.27 |
| [ Java ] 백준 11724번 연결 요소의 개수 (+DFS 이론 정리) (1) | 2024.02.18 |
